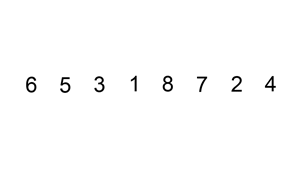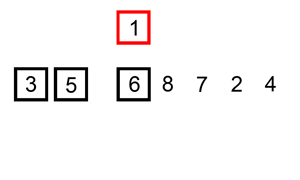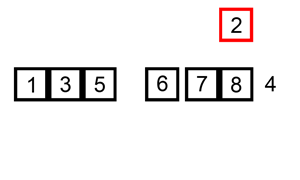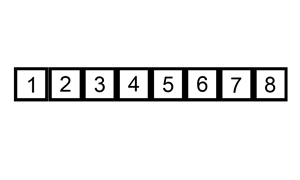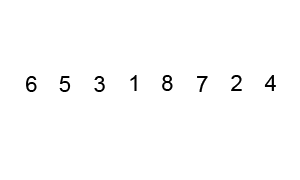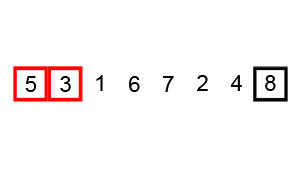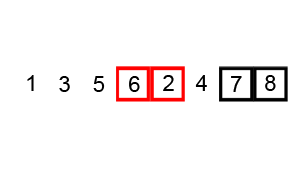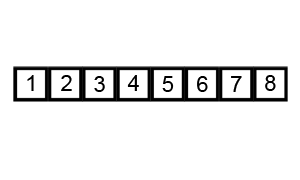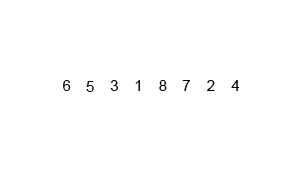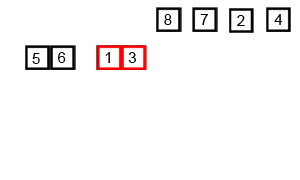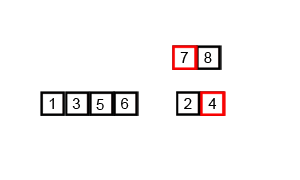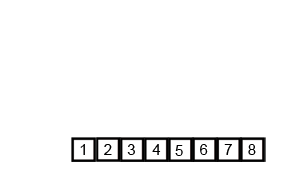python 数据结构之排序

在计算机科学中，排序更是随处可见。记录几个最常见的。

插入排序

这个其实就是打牌在起牌阶段整理手牌的过程，一般都是按照从小到大或者从大到小的顺序先拿着手牌，每次起一张新牌，会把牌“插入”到现有的手牌中，使得它比前面的牌大，比后面的牌小。
举个例子：

冒泡排序

在上第一节体育课的时候应该会先给大家排位置，冒泡排序的过程是这样的：第一个同学和第二个同学比一下身高，咦2比1低，高个往后排去，1和2交换位置，然后站在第二的同学再和站在第三的同学比个子，以此类推，一直到队尾，那么经过这一轮的交换，个子最高的同学肯定站在队尾了，接着在重头开始交换，直到排完队。

举个例子：

快速排序

可以说是最最经典的排序算法，没有之一。还是拿体育课排队来讲吧。体育老师随便抽了其中一个同学，然后对大家说：“比这个同学高的站在他右边，比他低的站在他左边”，经过这么一轮，可以肯定的是，左边的同学肯定比右边的同学都低。现在问题就变成了分别给左边和右边的同学排序。我们对左右两边的同学再用相同的方法，即从子队列中找一个同学，然后比他低的站左边，比他高的站右边。经过N多次这样的分组排序后，直到每个分组都排好序，那么整体的队列就排好序了。
举个例子：

归并排序
打牌都洗过牌吧，花式洗牌的一种，就是把一副牌分成两份，然后交叉洗进去，归并排序和这种洗牌方式很相近，原理都是把两部分牌洗在一起（归并在一起）只不过我们平常洗牌都是想把牌序打乱。假如让你把一副牌按照大小顺序洗好呢？我们可以每次把牌均分成两份，所谓一生二、二生四、四生八，把每份洗好，然后归并在一起，整副牌就洗好了。
举个例子：

Python3 代码实现：

插入排序

def insert_sort(origin_list):
    sorted_list = []
    for i in range(0, len(origin_list)):
        if len(sorted_list) == 0:
            sorted_list.append(origin_list[i])
            continue
        for j in range(len(sorted_list) - 1, -1, -1):
            if sorted_list[j] <= origin_list[i]:
                sorted_list.insert(j + 1, origin_list[i])
                break
            if j == 0:
                sorted_list.insert(j, origin_list[i])
    origin_list[:] = sorted_list[:]

origin_list = [5, 3, 1, 7, 9, 8]
insert_sort(origin_list)
print(origin_list)

冒泡排序

def bubble_sort(origin_list):
    for i in range(len(origin_list), 0, -1):
        for j in range(0, i - 1):
            if origin_list[j] > origin_list[j + 1]:
                origin_list[j], origin_list[j + 1] = origin_list[j + 1], origin_list[j]

origin_list = [5, 3, 1, 7, 9, 8]
bubble_sort(origin_list)
print(origin_list)

快速排序

def quick_sort(origin_list, start, end):
    if start >= end:
        return
    left = start
    right = end
    flag_index = left
    while left < right:
        while left < right:
            if origin_list[flag_index] > origin_list[right]:
                origin_list[flag_index], origin_list[right] = origin_list[right], origin_list[flag_index]
                flag_index = right
                break
            right -= 1
        while left < right:
            if origin_list[flag_index] < origin_list[left]:
                origin_list[flag_index], origin_list[left] = origin_list[left], origin_list[flag_index]
                flag_index = left
                break
            left += 1
        quick_sort(origin_list, start, flag_index)
        quick_sort(origin_list, flag_index + 1, end)
    return origin_list

origin_list = [5, 3, 1, 3, 7, 9, 8]
quick_sort(origin_list, 0, len(origin_list) - 1)
print(origin_list)

归并排序

def merge_sort(origin_list, start, end):
    if end <= start:
        return
    mid = (start + end) // 2
    merge_sort(origin_list, start, mid)
    merge_sort(origin_list, mid + 1, end)
    left_head = start
    right_head = mid + 1
    temp_list = []
    while left_head <= mid and right_head <= end:
        if origin_list[left_head] < origin_list[right_head]:
            temp_list.append(origin_list[left_head])
            left_head += 1
        if origin_list[left_head] >= origin_list[right_head]:
            temp_list.append(origin_list[right_head])
            right_head += 1
    if left_head <= mid:
        temp_list += origin_list[left_head:mid + 1]
    if right_head <= end:
        temp_list += origin_list[right_head:end + 1]
    for i in range(0, len(temp_list)):
        origin_list[i + start] = temp_list[i]

origin_list = [5, 3, 1, 3, 7, 9, 8]
merge_sort(origin_list, 0, len(origin_list) - 1)
print(origin_list)

二分法查找

def binary_search(search_list, target):
    left = 0
    right = len(search_list) - 1
    while left <= right:
        mid = (left + right) // 2
        if search_list[mid] < target:
            left = mid + 1
            continue
        if search_list[mid] == target:
            return mid
        if search_list[mid] > target:
            right = mid - 1
            continue
    return None
search_list = [1, 3, 4, 6, 8, 9]
print(binary_search(search_list, 5))
print(binary_search(search_list, 1))
print(binary_search(search_list, 3))
print(binary_search(search_list, 4))
print(binary_search(search_list, 6))
print(binary_search(search_list, 8))
print(binary_search(search_list, 9))