python 数据结构之树

用Python实现二叉树 遍历

树都是从一个主干根，然后往上分叉，每个枝杈又会分枝杈，而在计算机科学中，树则是可以看做一个倒挂的树，根在最上面，往下开叉，如下图:

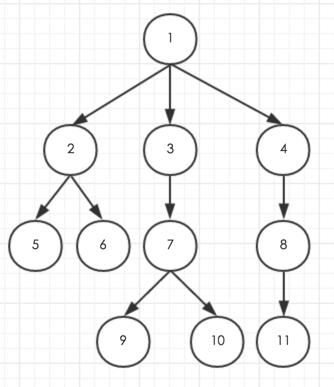
从这个图来看：

• 1节点就是根节点
• 从1分叉出了2、3、4节点。
• 2、3、4是1的孩子节点。
• 2、3、4互为兄弟节点。
• 1为2、3、4的父节点。
• 5、6是2的子节点。
• 这棵树深度是4（一共4层）
• 多棵树组成森林

二叉树

二叉树是每个节点最多有两个子节点的树，举个例子：

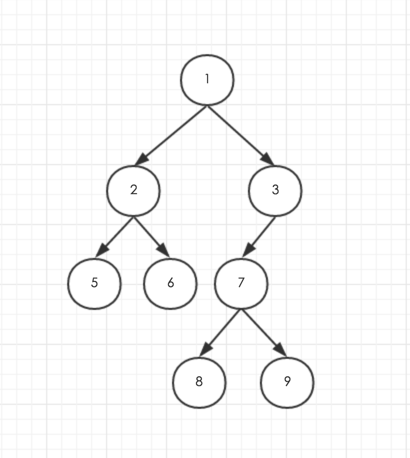
遍历

前序遍历（根左右）
还是以上图为例，前序遍历顺序是：
[1, 2, 5, 6, 3, 7, 8, 9]

中序遍历（左根右）
还是以上图为例，中序遍历顺序是：
[5, 2, 6, 1, 8, 7, 9, 3]

后续遍历（左右根）
还是以上图为例，后序遍历顺序是：
[5, 6, 2, 8, 9, 7 ,3, 1]

python实现二叉树

class Node(object):
    def __init__(self, index):
        self.index = index
        self.left_child = None
        self.right_child = None

class Binary_tree(object):
    def __init__(self, root):
        self.root = root

    # 前序遍历（根左右）
    def pre_travel(self, node):
        if not node:
            return
        print(node.index, end=' ')
        self.pre_travel(node.left_child)
        self.pre_travel(node.right_child)

    # 中序遍历（左根右）
    def mid_travel(self, node):
        if not node:
            return
        self.mid_travel(node.left_child)
        print(node.index, end=' ')
        self.mid_travel(node.right_child)

    # 后续遍历（左右根）
    def back_travel(self, node):
        if not node:
            return
        self.back_travel(node.left_child)
        self.back_travel(node.right_child)
        print(node.index, end=' ')


node_dict = {}
for i in range(1, 10):
    node_dict[i] = Node(i)
node_dict[1].left_child = node_dict[2]
node_dict[1].right_child = node_dict[3]
node_dict[2].left_child = node_dict[5]
node_dict[2].right_child = node_dict[6]
node_dict[3].left_child = node_dict[7]
node_dict[7].left_child = node_dict[8]
node_dict[7].right_child = node_dict[9]

tree = Binary_tree(node_dict[1])
print('前序遍历:')
tree.pre_travel(tree.root)
print('\n')
print('中序遍历:')
tree.mid_travel(tree.root)
print('\n')
print('后序遍历:')
tree.back_travel(tree.root)
print('\n')

输出:

前序遍历:
1 2 5 6 3 7 8 9 

中序遍历:
5 2 6 1 8 7 9 3 

后序遍历:
5 6 2 8 9 7 3 1